An In-Depth Look At Data Preparation For Machine Learning
An in-depth exploration of data cleaning and feature engineering, feature selection and dimensionality reduction, and data transformation
In this installment of the Decoding Biology newsletter, we’ll take an in-depth look at data preparation with topics ranging from data cleaning, feature engineering, feature selection and dimensionality reduction, and data transformation.
If you enjoy this newsletter, don’t forget to leave a like ❤️. It helps more people discover this Decoding Biology on Substack. The button is located towards the bottom of this newsletter.
🧬 What Is Data Preparation?
It's a common misconception that once you've created a few effective machine-learn model pipelines, you can reuse them repeatedly without fail or take any off-the-shelf model and use it in your own project without modification. These misconceptions stem from an underappreciated aspect of machine learning modes: data is a fundamental component of the model, not something you feed into the model to produce a given output. In fact, data is one of the sole differentiating features between machine learning projects, and as a consequence, data preparation is the lifeblood of any machine learning system you construct.
“Practitioners agree that the vast majority of time in building a machine learning pipeline is spent on feature engineering and data cleaning. Yet, despite its importance, the topic is rarely discussed on its own.”
-Zheng & Casari (2018). Feature Engineering For Machine Learning: Principles And Techniques For Data Scientists
In a previous article titled Introduction To Data Pre-processing, I stated, "Data pre-processing is a critical step in the data analysis process, where raw data is transformed into a format compatible with a specific, selected, machine learning algorithm."
Data preparation is essential because most machine learning algorithms make assumptions about the data you feed them. More specifically, machine learning algorithms generally require input data to be numerical. As a result, if your input data contains values that aren't numbers, you will need to turn them into numbers (i.e., changing yes and no to 0 and 1). In addition, certain machine learning algorithms may also make assumptions about the scale, probability distribution, and statistical relationships between input variables.
It's up to you to know the assumptions of your model and how your data is structured. Only then can you prepare your data in such as way as to best expose the underlying structure of your prediction problem to your learning algorithms in order to achieve the best performance (given a finite number of resources).
🧬 Where Does Data Preparation Fit Into The Big Picture?
Up to 80% of data scientist's time is often spent preparing data. Additionally, since data preparation is a prerequisite to the rest of a machine learning workflow, data scientists and engineers working on machine learning problems must become proficient with data peroration techniques. Thus, it's important to understand where data preparation fits in the grand scheme when developing a machine learning system.
Below you'll find a concept model showing how the various processes within our system interact:
Importantly, you’ll notice sections of the model at various time-points labeled ‘clean data’, ‘feature selection’, and ‘transform data’. These are all parts of the data preparation process! Thus, it’s important to realize that data preparation isn’t a one-and-done task you check off at the start of a project - instead it’s an iterative process that you’ll engage in throughout your working on a project.
I tend to break the data preparation process down into three components:
Data Cleaning and Feature Engineering: I think of data cleaning and feature engineering as subtraction and addition, respectively.
Data cleaning is the process of identifying and correcting errors in your data. I prefer to perform data cleaning after data visualization since the latter allows me to see outliers or anomalies in my data and remove them where needed.
Feature Engineering, on the other hand, is all about using domain-specific knowledge to ‘engineer’ input data (features) in ways that enhance a model’s performance - this could mean creating a composite feature that uniquely combines two existing features, or using two current features to calculate a new third feature.
Feature Selection and Dimensionality Reduction: feature selection and dimensionality reduction are both techniques used to reduce the number of different input variables in a dataset.
Certain algorithms perform poorly when input variables are irrelevant to the output (i.e., target) variable. Feature Selection is the process of identifying input variables (i.e., features) that are most relevant to a given problem and removing input variables that lack relevance.
Dimensionality Reduction is a data preparation technique that compresses high-dimensional data into a lower-dimensional space while preserving the integrity of the data, reducing the number of input variables in the process.
Data Transformations , which are used to change the scale or distribution of a selected features. For example, standardization is a data transformation technique that centers the distribution of data attributes such that their means and standard deviations are equal.
🧬 Data Cleaning And Feature Engineering
As previously stated, data cleaning and feature engineering can be thought of as subtractive and additive processes, respectively. Data cleaning is the process of identifying and correcting systematic errors in messy data. For example, data cleaning includes tasks such as correcting mistyped data, removing corrupted or missing (i.e., null) data points, removing duplicate data, and sometimes adding missing data values. Data cleaning may also include tasks such as encoding categorical variables into integer variables (i.e., turning no/maybe/yes into 0/1/2) or categorical variables in binary variables (i.e., turning male/female into 0/1).
For what seems like a rote task, data cleaning often requires a high degree of domain expertise. For example, let’s say you have a dataset and VO2 (i.e., volume of oxygen consumption) as one of your features. You may notice a row of data with a VO2 value of 92. As a subject matter expert, you may quickly realize how improbable this value is, whereas someone without domain-specific knowledge of the various measurements may overlook this.
However, in this newsletter, i’m going to focus on three basic data-cleaning operations that you’re likely to encounter in the bulk of your machine-learning projects, including encoding categorical variables, removing zero-variance predictors, and removing both null and duplicate values form your dataset. Below you’ll find a short description of each of these tasks plus a few best practices for completed them:
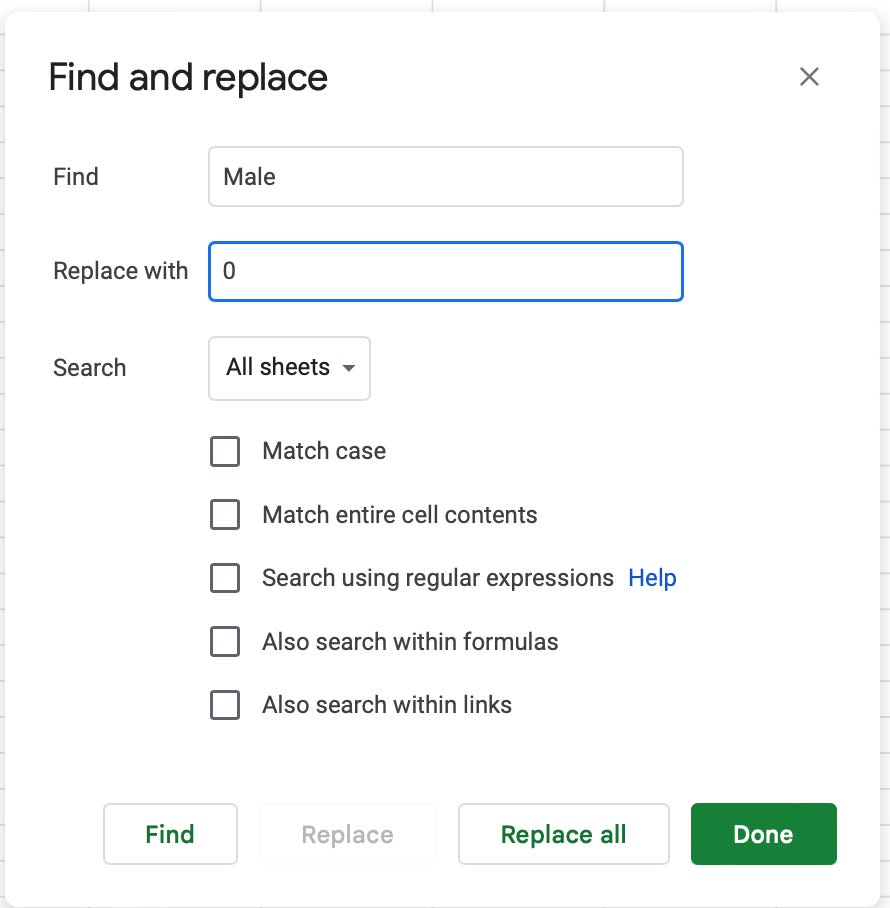
Encoding categorical variables: many machine learning algorithms require inputs to be numerical values, and as a result, a common data cleaning task involves encoding categorical variables into numerical and/or binary variables. For example, turning male and female into 0 and 1. These changes can be made to the CSV directly using the Find and Replace function in Excel, as demonstrated below, or they can be made in your coding notebook:
Removing zero-variance predictors: zero-variance predictors are input variables where all instances (i.e., rows of data) contain the same value. Inputs without variance offer no predictive value and can be identified with Panda’s nunique() function (zero variance predictors will have one unique value).
Removing null and duplicate values: rows of data containing no input or duplicated input values offer no predictive value and may hurt model performance. Null values can easily be removed with the dropna() function, while duplicate rows can be removed with the drop_duplicates() function.
The above list of data cleaning procedures is not inclusive and is meant to get you started in thinking about data cleaning. Personally, I do the bulk of my data cleaning in Excel before uploading a CSV file with my data to a Juypter or Google Collab notebook. Then I’ll use functions like dropna() and drop_duplicates() to automate more tedious tasks.
Please share any specific data-cleaning tips and tricks you frequently use in the comment section below!
As previously mentioned, data cleaning and feature engineering are two sides of the same coin. Feature engineering is the process of using domain-specific knowledge to create new input variables from the available data in a given dataset to enhance a model’s performance. This may mean creating a composite feature that uniquely combines existing features or using two or more existing features to calculate a new feature. For example, imagine you have data from a wearable device, and in your dataset, you see three features titled “x_acceleration”, “y_acceleration”, and “z_acceleration,” respectively. With background knowledge, you may realize you could engineer a new feature called “total_acceleration,” which is calculated as follows: √(x_acceleration^2 +y_acceleration^2 + z_acceleration^2).
Engineering new features is highly specific to a given data set, so it is difficult to generalize best practices. As a result, I’ll save this topic for a dedicated future newsletter.
🧬 Feature Selection And Dimensionality Reduction
Feature selection is the process of selecting features in a given dataset that best contribute to predicting the desired outcome variable in your model and removing redundant or irrelevant features that decrease the accuracy of your model’s predictions. As a general rule of thumb, using only as much data is necessary to make a prediction is desirable, and we should strive to produce the simplest well-performing model.
“Many models, especially those based on regression slopes and intercepts, will estimate parameters for every term in the model. Because of this, the presence of non- informative variables can add uncertainty to the predictions and reduce the overall effectiveness of the model.”
-Kuhn & Johnson (2013). Applied Predictive Modeling
Feature selection techniques are subdivided into two major groups: those that use the target variable to select features (supervised learning) and those that do not (unsupervised learning). In this newsletter, I will only discuss supervised learning methods, which can be further divided into filter, wrapper, and intrinsic methods.
Filter-based feature selection methods use statistical tests to score the correlation between input variables (i.e., features) and the selected output variable (i.e., target) and select the features that have the strongest relationship with the target.
Filter-based methods are fast and effective, but the choice of statistical tests used to score features depends on both the input and output data types. As a result, it can be challenging to select appropriate statistical measures when performing filter-based feature selection. The chart below provides a simple heuristic for selecting appropriate statical tests for filter-based methods:
The chart above is specific to situations where you have all numerical input variables. However, there will be situations where you have all categorical input variables (this is rare) or multiple different types of input variables (less rare). In these instances, you can separately select numerical and categorical features using appropriate statistical tests or utilize wrapper-based selection methods, which we’ll cover shortly.
An example filter method is SelectKBest. Below is an example code using the SelectKBest method to select features in the Oasis-1 dataset1. In this case, we’re using the ANOVA F-value as our statistical measure since we have numerical inputs with a categorical output:
Which results in the following scores (a higher score is better, which means that MMSE, nWBV, and age have the strongest relationship to CDR based on the results of our selected statistical test.):
Unlike filter-based feature selection methods, wrapper methods explicitly choose features that result in the best-performing model. Wrapper feature selection methods create many different models with different sets of input features and then select the features that result in the best-performing model. The advantage of wrapped-based methods is that they are unconcerned with data types, making them easy to implement for practitioners. However, wrapper methods are more computationally expensive.
An example wrapper method is recursive feature elimination, which considers a subset of features, runs your chosen machine learning algorithm, gauges model performance, and repeats this process until an optimal set of features is found.
An example wrapper method is recursive feature selection (RFE), which eliminates the least valuable features in a dataset one by one until a specified number of strong features remain. Recursive feature elimination is a popular feature selection technique because it’s easy to configure and understand the results, and it’s effective for selecting input features that are most relevant for predicting the target variable.
Recursive feature elimination works by removing attributes and then building a model around those that remain, using model accuracy to figure out which attributes, or combinations of attributes, result in the most accurate predictions. Additionally, two hyper-parameters can be configured during recursive feature elimination, which will impact your results: the specific algorithm used to select featured and the number of features to you want to select.
In the code example below I run a logic regression-based model and use RFE to select the four best input variables for enhancing my model’s predictive performance.
Which results in the following scores (the selected features are labeled True and the eliminated features are labeled False):

Intrinsic methods automatically select features as part of fitting the chosen machine learning model and include machine learning algorithms such classification and regression trees. In the code example below I demonstrate how to use a Decision Tree Regressor to select features in our dataset:
Feature selection with a Decision Tree Regressor produces the following result (a higher score is better, thus MMSE is the best performing feature with age as a distant second):
We can also use a Random Forrest Regressor to select features in our dataset as well, which is another intrinsic feature selection method:
Which produces the following output (a higher score is better, thus MMSE is the best performing feature with eTIV as a distant second):
A related concept to feature selection is that of dimensionality reduction. Dimensionality Reduction is a data preparation technique that compresses high-dimensional data into a lower-dimensional space, reducing the number of input variables. The key difference between feature selection and dimensionality reduction is that feature selection decides which input variables to keep or remove from the dataset. In contrast, dimensionality reduction creates a projection of the data resulting in entirely new input features.
Unlike feature selection, the variables you are left with after performing dimensionality reduction are not directly related to the original input variables (i.e., features), making it difficult to interpret the results. As such, dimensionality reduction is an alternative to feature selection rather than a type of feature selection.
For simplicity's sake, you can think of dimensions as the number of input features in a dataset. Many issues can arise when analyzing high-dimensional data that otherwise wouldn't be an issue in lower-dimensional space. This problem is called the curse of dimensionality and is the reason we employ dimensionality reduction techniques, such as principle component analysis (PCA).
Principal component analysis (PCA) is an unsupervised learning technique that uses linear algebra to reduce the dimensionality of a dataset by removing linear dependencies (i.e., strong correlations) between input variables. Reducing the dimensionality of a dataset results in fewer input values, which simplifies predictive models and helps them perform better on unseen data.
An important property of principal component analysis is the ability to choose the number of dimensions (i.e., principal components) the dataset will have after the algorithm has transformed it. Below you'll find sample code performing principal component analysis on the OASIS-1 dataset:
Which results in the following output:
Again, it's important to note that principal components are not features in your original dataset. Instead, a principal component can include attributes from multiple different features. Thus, principal component analysis aims to tell you what percent of the variance each principal component accounts for in your target outcome. In this specific case, the first principal component accounts for 99% of the target's variance (which is much higher than is normally the case).
🧬 Data Transformation
Many machine learning algorithms perform better when numerical input variables in your dataset are scaled to a standard range. For example, algorithms that use a weighted sum of input variables, such as linear regression, logistic regression, and deep learning, are impacted by the scale of input data.
Additionally, algorithms that rely on distance measures between samples, such as k-nearest neighbors (KNN) and support vector machines (SVM), are also impacted. On the flip side, algorithms such as CART (i.e., classification and regression trees) and ensembles of trees (i.e., random forest regression) are unimpacted by the scale of data. However, it is nearly always advantageous to scale numerical input values to a standard range, hence the need for data transformation techniques.
Data transformation is a process used to change a given dataset's scale or distribution of features. The two primary techniques used to change the scale of data are standardization transforms and normalization transforms, which I've covered in depth in a previous newsletter titled, Introduction To Data Pre-Processing.
Standardization is used to transform data attributes with a Gaussian (i.e., normal) distribution and differing means and standard deviations, so all attributes have a mean of 0 and a standard deviation of 1. Additionally, standardization is most suitable when performing linear regression, logistic regression, or linear discriminate analysis.
The formula for data standardization is as follows:
Standardized value = (valueᵢ - mean) / standard deviation
where mean and standard deviation are calculated as follows:
mean = Σ valueᵢ / count(values)
standard deviation = √(Σ (valuesᵢ - mean)² / counts(values)-1)
Below you'll find sample code demonstrating a standardization technique using the Pima Diabetes dataset followed by the first few rows of standardized data:
Normalization (re-scaling) is best used when your input data contains attributes with varying scales. For example, if one attribute has values ranging from 0-20, while another has values ranging from 655-9023. In these cases, normalization puts all data attributes on the same scale, which is usually 0-1.
Normalization is best used for optimization algorithms such as gradient descent. However, it can also be used before algorithms that weigh inputs, such as neural networks, and algorithms that use distance components, such as k-nearest neighbors (KNN).
The formula for data rescaling (normalization) is as follows:
normalized value = (valueᵢ - min) / (max - min)
Below you'll find sample code demonstrating a normalization technique using the Pima Diabetes dataset, followed by the first few rows of normalized data:
Whereas standardization and normalization are used to alter the scale of data, power transforms and quantile transforms are used the change the data’s distribution.
Power transforms are used to change on input variables that are nearly Gaussian, but slightly skewed, and make them Gaussian. Power transforms are useful since many algorithms such as gaussian naive bayes, or even simple linear regression, assume that numerical input variables have a Gaussian (i.e., normal) distribution . Thus, using a power transform can improve your model’s performance when the input variables are skewed towards a non-gaussian probability distribution.
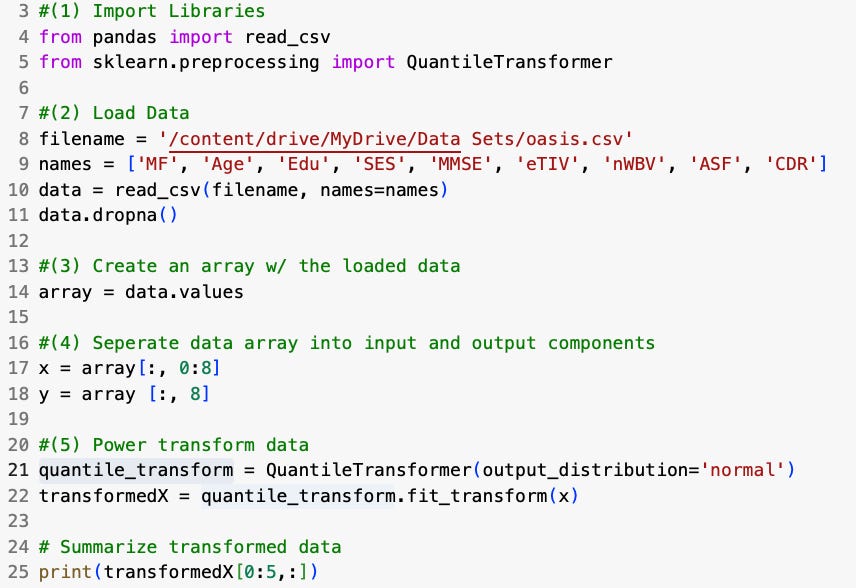
Below you'll find sample code demonstrating a power transformation technique using the Oasis-1 dataset:
Quantile transforms, on the other hand, are used to force variables with unusual ‘organic’ distributions into uniform or Gaussian distribution patterns. For example, it’s a common practice to use a quantile transform on input variables with outlier values since ordinary standardization techniques can skew the data in a maladaptive manner.
Below you'll find sample code demonstrating a quantile transformation technique using the Oasis-1 dataset:
👉 If you have any questions about the content in this newsletter please let me know in the comment section below.
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack. The button is located towards the bottom of this email.
👉 If you enjoy reading this newsletter, please share it with friends!
The Oasis-1 dataset consists of a cross-sectional collection of 416 subjects aged 18 to 96. For each subject, 3 or 4 individual T1-weighted MRI scans obtained in single scan sessions are included. The subjects are all right-handed and include both men and women. 100 of the included subjects over the age of 60 have been clinically diagnosed with very mild to moderate Alzheimer’s disease (AD). Additionally, a reliability data set is included containing 20 nondemented subjects imaged on a subsequent visit within 90 days of their initial session.
Citation: OASIS-1: Cross-Sectional: Principal Investigators: D. Marcus, R, Buckner, J, Csernansky J. Morris; P50 AG05681, P01 AG03991, P01 AG026276, R01 AG021910, P20 MH071616, U24 RR021382