Understanding Mutual Information in Bioinformatics

A Deep Dive into Entropy, Mutual Information, and Their Application in Gene Expression Analysis

Decoding Biology Shorts is a new weekly newsletter sharing tips, tricks, and lessons in bioinformatics. Enjoyed this piece? Show your support by tapping the ❤️ in the header above. Your small gesture goes a long way in helping me understand what resonates with you and in growing this newsletter. Thank you!

---

Understanding Mutual Information in Bioinformatics

Studying causality in biology is challenging because biological systems are incredibly complex, making it hard to definitively prove that one thing directly causes another.

Studying mutual dependence between two variables is often easier than studying causality, and can convey some of the same information. For example, we may investigate the likelihood that a particular gene is expressed, given that other specific genes are also expressed. Understanding gene co-expression in this way can help us uncover the structure of biological pathways and provide insights into diseases like cancer, where coordinated gene expression plays a critical role.

In bioinformatics, the relationship between variables—whether genes, proteins, or other biological factors—can be explored using the framework of information theory, a field developed by Claude Shannon. Information theory originally focused on the reliability of communication through noisy channels, but its principles can also be applied to questions of dependency in biological systems. For example, it can help us answer questions like: How likely is it that one variable X is "on" (present), while another variable Y is either "on" (present) or "off" (absent)?

Mutual Information: Quantifying Dependence

When we say two variables are "coupled," we refer to the degree to which they are related. If two variables, X and Y, are perfectly coupled, they will either both be "on" (expressed), both be "off" (not expressed), or one will be "on" while the other is "off." However, in biological data, perfect coupling is rare. As a result, it is often challenging to determine how one variable influences the other, or whether they are related at all.

The concept of mutual information allows us to quantify the dependence between two variables, X and Y, regardless of whether the coupling is perfect, strong, weak, or absent. In simple terms, mutual information measures the extent to which knowledge about one variable reduces the uncertainty of the other.

For instance, if X and Y are completely independent, the mutual information between them is zero because knowing everything about one variable won't help predict the state of the other. Conversely, if X and Y are strongly dependent, their mutual information will be high.

Entropy: The Foundation of Mutual Information

To calculate mutual information, we first need to understand entropy. Entropy, denoted H(X), measures the uncertainty associated with a random variable X. In biological terms, this uncertainty could represent how unpredictable the expression level of a gene is, given that it can take various values (e.g., expressed, not expressed) with specific probabilities.

Importantly, the uncertainty of X may depend on what we know about another variable, Y. This relationship is quantified by conditional entropy, denoted H(X∣Y), which measures the remaining uncertainty of X after accounting for knowledge of Y.

Joint Entropy: Combining Uncertainty

The uncertainty of a pair of variables X and Y is quantified by joint entropy, denoted H(X,Y). Joint entropy represents the total uncertainty of both variables, taking into account both individual uncertainties and their interaction. It can be expressed as the sum of the individual entropies and the conditional entropy:

H(X,Y)=H(X)+H(Y∣X)=H(Y)+H(X∣Y)

This equation shows the relationship between the uncertainty of X, Y, and how the uncertainty of one variable is influenced by the other.

Calculating Mutual Information

Finally, mutual information I(X;Y) is the measure of the shared information between two variables. It is calculated as the sum of the individual entropies minus the joint entropy:

I(X;Y)=[H(X)+H(Y)]−H(X,Y)

This equation tells us how much knowing one variable reduces the uncertainty about the other. In bioinformatics, mutual information is widely used to explore the relationships between genes, proteins, and other biological data, providing valuable insights into how these elements interact and co-vary within biological systems.

Case Study: Calculating Mutual Information Between Gene Expression Levels

Let's consider a case where we have gene expression data from a group of samples, and we want to examine the mutual dependence between the expression levels of two genes, Gene A and Gene B. We can compute the mutual information between their expression levels to understand how strongly these genes are co-expressed.

Step 1: Install Necessary Libraries

We will use the sklearn library for mutual information calculations, pandas for data manipulation, numpy for generating synthetic data, and matplotlib for plotting.

from sklearn.feature_selection import mutual_info_regression
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

Step 2: Generate or Load Gene Expression Data

For simplicity, let’s generate synthetic gene expression data. In real scenarios, you would typically load data from an expression matrix (e.g., from RNA-Seq results).

# Simulating gene expression levels for 100 samples
np.random.seed(42)
gene_a_expression = np.random.rand(100)  # Random expression levels for Gene A
gene_b_expression = gene_a_expression + 0.2 * np.random.randn(100)  # Gene B expression is somewhat correlated with Gene A

# Creating a DataFrame to hold the data
data = pd.DataFrame({
    'Gene_A': gene_a_expression,
    'Gene_B': gene_b_expression})

# Displaying the first few rows of the data
print(data.head())

Which produces the following output:

Step 3: Calculate Mutual Information

Now, we can compute the mutual information between the expression levels of Gene A and Gene B. Since mutual information can be applied to continuous variables, we will use the mutual_info_regression function from sklearn, as demonstrated below:

# Reshape the data into two-dimensional arrays (required for mutual_info_regression)
X = data[['Gene_A']]
y = data['Gene_B']

# Calculate mutual information
mi = mutual_info_regression(X, y)

# Print the mutual information
print(f"Mutual Information between Gene A and Gene B: {mi[0]:.4f}")

The mutual information value will give us a measure of the shared information between the two genes. A higher value indicates a stronger dependence between the gene expression levels. After running the code block above, I get the output:

Mutual Information between Gene A and Gene B: 0.5044

This means that there is a moderate amount of shared information between Gene A and Gene B. While they are related (since we introduced a correlation in the synthetic data), the mutual information is not close to 1, indicating that their relationship is not perfectly coupled.

Step 4: Visualizing the Relationship

It is often useful to visualize the relationship between two variables. Let’s plot the expression levels of both genes.

plt.scatter(data['Gene_A'], data['Gene_B'], alpha=0.7)
plt.xlabel('Gene A Expression Level')
plt.ylabel('Gene B Expression Level')
plt.title('Gene A vs Gene B Expression')
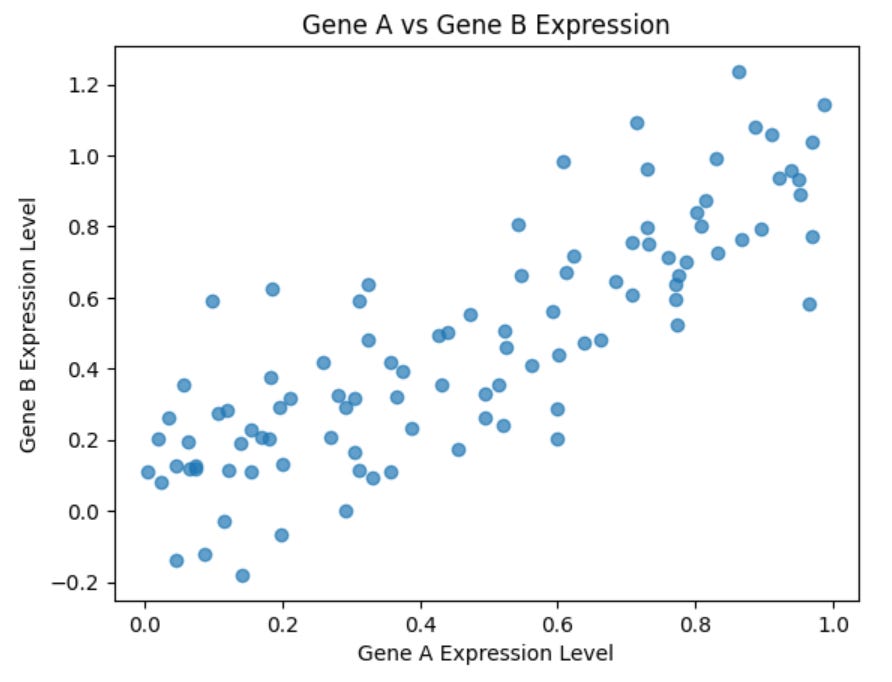
plt.show()

Which produces the following plot:

This scatter plot will help you visually assess the relationship between the two genes. A linear or clustered pattern might indicate a strong mutual dependence, while a more dispersed pattern would suggest a weaker relationship.

In this case study, we demonstrated how to calculate the mutual information between two genes' expression levels. By using the mutual_info_regression function from sklearn, we were able to quantify the degree of dependence between the two genes. Visualizing the data further aids in understanding the nature of their relationship. This method can be extended to larger datasets to explore gene co-expression or to study the interactions between other biological variables.

---